Solar system objects move across the image during an exposure. If the movement is significant, the signal to noise ratio of the object decreases compared to an equivalent stationary object.
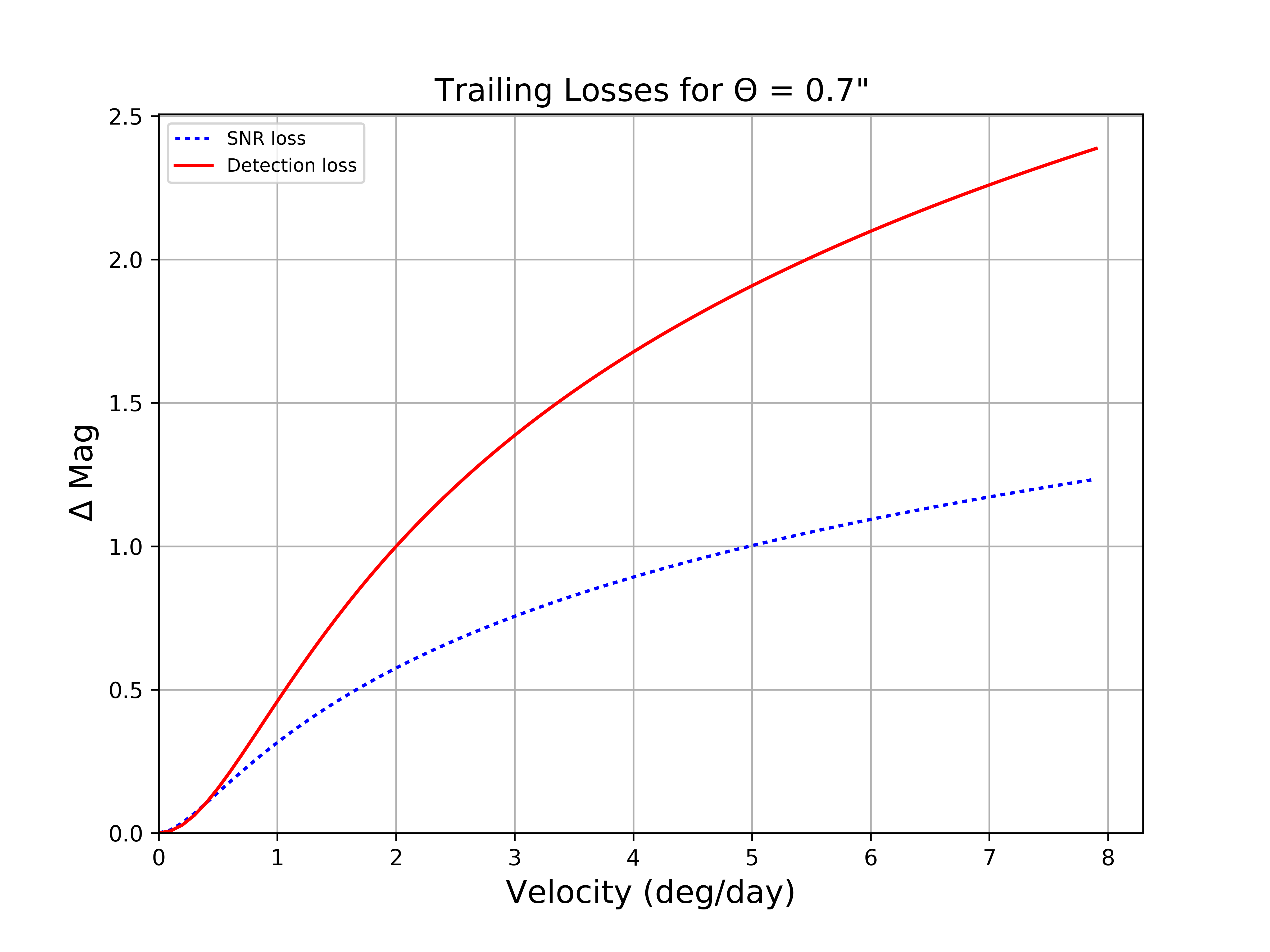
Figure 1 Trailing losses in 0.7” seeing for 30 second exposures. The blue dotted line (SNR loss) indicates the losses due to simply spreading the light from a moving source over more background pixels. The red line (Detection loss) indicates the losses due to detection algorithms assuming a stellar PSF instead of a trailed PSF. With additional work in the source detection software stage, detection losses can be mitigated to the level of SNR losses.
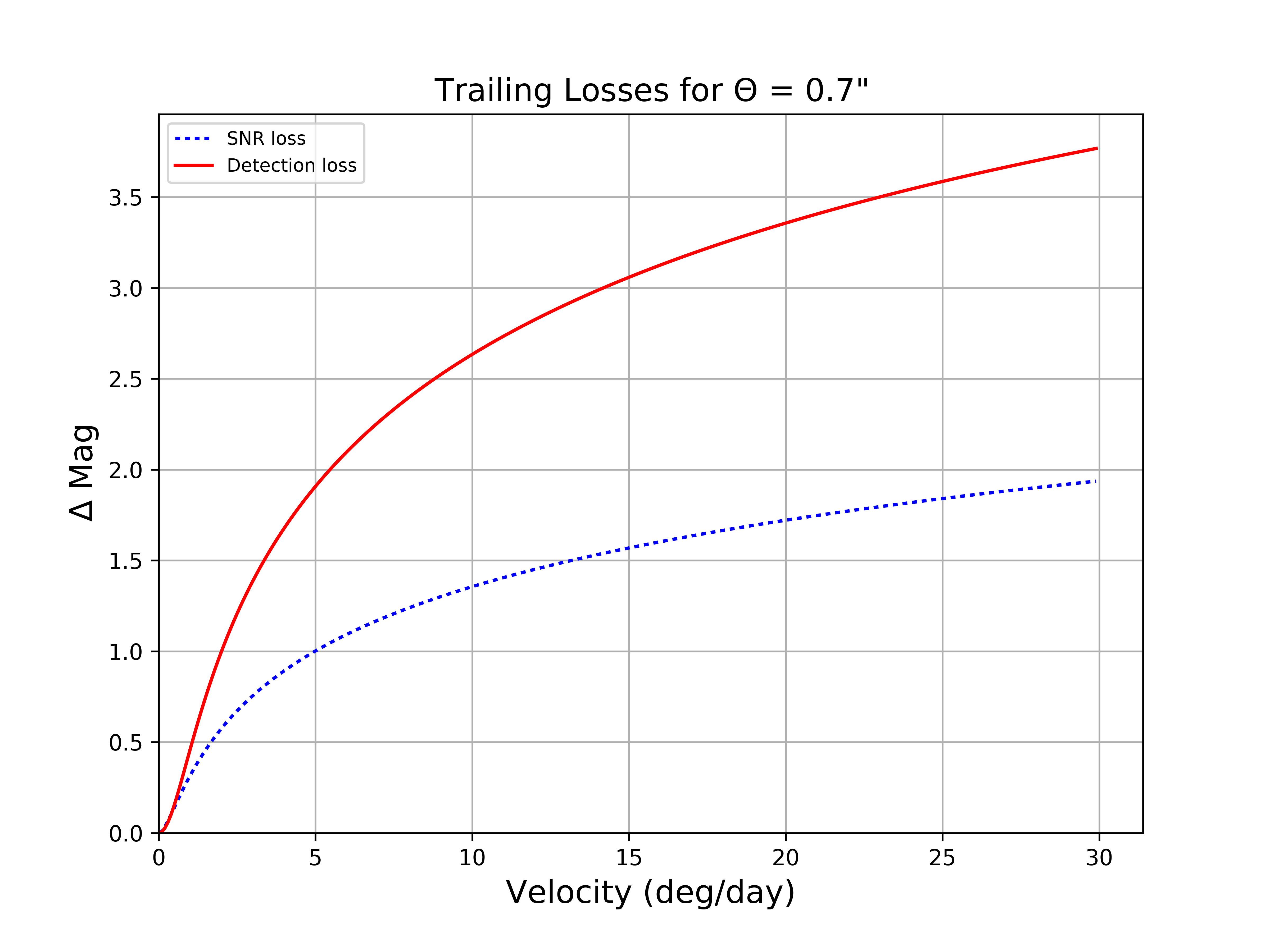
Figure 2 Trailing losses in 0.7” seeing for 30 second exposures, as above, but with a wider range of velocities.
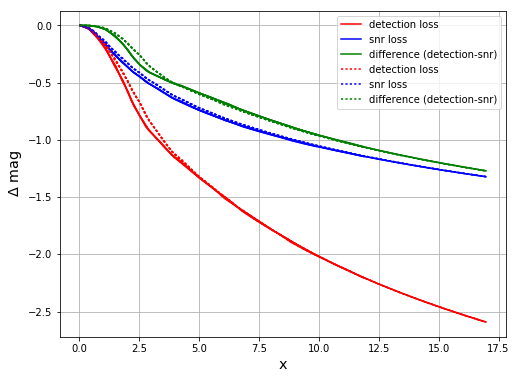
Figure 3 Trailing losses as a function of “X” = velocity(deg/day) * exposure time(s) / seeing(”) / 24.0.
def trailing_losses(velocity, seeing, texp=30.):
"""Calculate detection-based and SNR-based trailing losses.
Parameters
==========
velocity : float
The velocity of the moving object, in deg/day.
seeing : float
The seeing in the image, in arcseconds.
texp : float, opt
The exposure time, in seconds.
Returns
=======
dict
dmag['trail'] and dmag['detect'] - detection and SNR losses.
"""
a_trail = 0.761
b_trail = 1.162
a_det = 0.420
b_det = 0.003
x = velocity * texp / seeing / 24.0
dmag = {}
dmag['trail'] = 1.25 * np.log10(1 + a_trail*x**2/(1+b_trail*x))
dmag['detect'] = 1.25 * np.log10(1 + a_det*x**2 / (1+b_det*x))
return dmag
Note
This technote is not yet published.
Calculating trailing losses for moving objects.